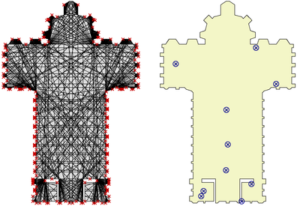
In this project, we initially studied the Art Gallery Problem (AGP) with vertex guards, whose goal is to minimize the number of vertex guards required to watch an art gallery whose boundary is an \(n\)-vertex polygon. Unlike other works that have appeared in the literature, the objective here was to design an exact algorithm. We designed an algorithm that iteratively computes optimal solutions to Set Cover Problems (SCPs) corresponding to discretization of \(P\). While it is shown [1] that this procedure converges to an exact solution of the original continuous problem, the number of iterations executed is highly dependent on the way we discretized the polygon. Although the best theoretical bound for convergence is \(O(n^3)\) iterations, we show that, in practice, it is achieved after a small number of them, even for random polygons of thousands of vertices.
After 2011, we started working on the Art Gallery Problem with Point Guards, which is a more general version of the AGP, where the guards may be positioned at any point in the interior or on the boundary of the input polygon. As before, we seek to find exact solutions. An algorithm has been implemented and tested, which solves to optimality a very large collection of polygons (with and without holes) of multiple classes [2].
Related Publications
- M. C. Couto, P. J. de Rezende and C. C. de Souza,
An exact algorithm for minimizing vertex guards on art galleries, 2011, ITOR.
https://onlinelibrary.wiley.com/doi/10.1111/j.1475-3995.2011.00804.x/full - D. C. Tozoni, P. J. de Rezende and C. C. de Souza,
The Quest for Optimal Solutions for the Art Gallery Problem: A Practical Iterative Algorithm, 2013, SEA.
https://dx.doi.org/10.1007/978-3-642-38527-8_29
