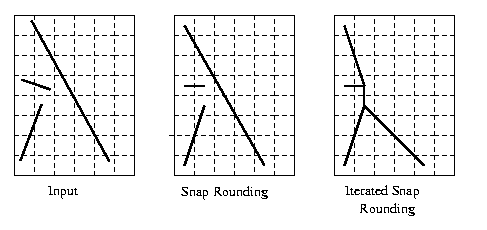
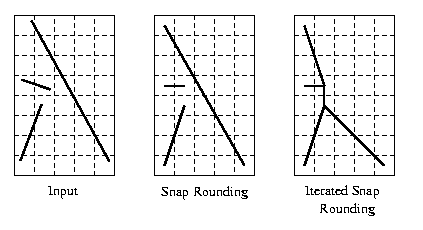
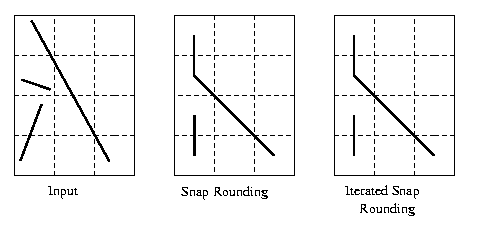
Snap rounding is a well known method for converting arbitrary-precision arrangements of segments into a fixed-precision representation.
Given an arrangement of segments whose vertices (end-points and intersections) are represented with arbitrary-precision coordinates, snap rounding proceeds as follows. We tile the plane with a grid of unit squares, pixels, each centered at a point with integer coordinates. A pixel is hot if it contains a vertex of the arrangement. Each vertex of the arrangement is replaced by the center of the hot pixel containing it and each edge e is replaced by the polygonal chain through the centers of the hot pixels met by \(e\), in the same order as they are met by \(e\).
In a snap-rounded arrangement, the distance between a vertex and a non-incident edge can be extremely small compared with the width of a pixel in the grid used for rounding. Iterated Snap Rounding is a technique which rounds the arrangement in a similar way as Snap Rounding, but makes sure each vertex is at least half-the-width-of-a-pixel away from any non-incident edge. Iterated Snap Rounding preserves the topology of the original arrangement in the same sense that the original scheme does. However, the guaranteed quality of the approximation degrades. Thus each scheme may be suitable in different situations.
We implemented both schemes. We have examples that demonstrate the difference in rounding between the schemes (see below).
 |
Examples
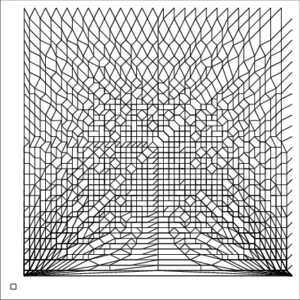
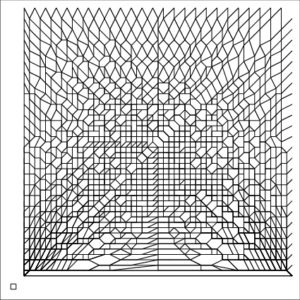
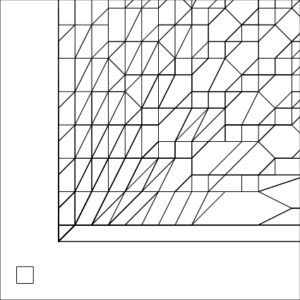
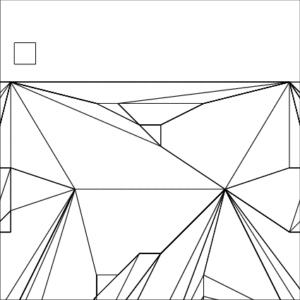
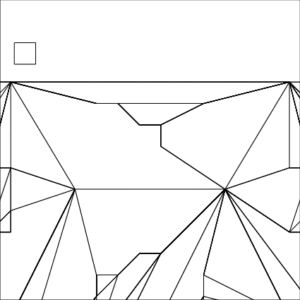
Example 1—Congestion
|
|
|
|
| The small square inside each image represents a unit pixel | ||
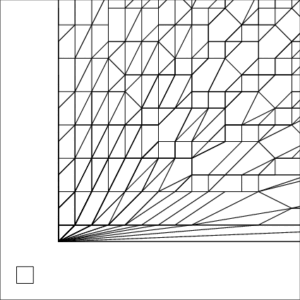
Example 1 Zoomed In
|
|
|
|
| The small square inside each image represents a unit pixel | ||
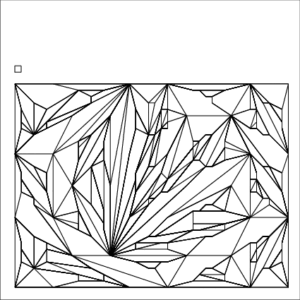
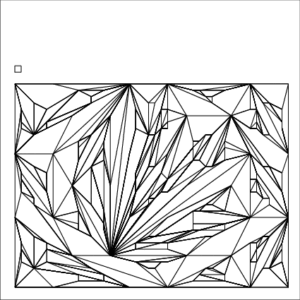
Example 2—Triangulation
Iterated Snap Rounding—Example 2 : Triangulation
|
|
|
|
| The small square inside each image represents a unit pixel | ||
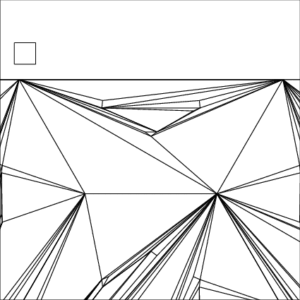
Example 2 Zoomed In
|
|
|
|
| The small square inside each image represents a unit pixel | ||
Example 3—Pixel Size
Iterated Snap Rounding – Example 3: Pixel Size
Choose Pixel Size
0.5 / 1 / 2
Pixel size = 0.5
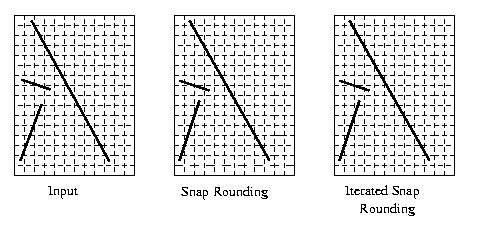
pixel size = 1
pixel size = 2