We present a simple and natural extension of the multi-robot motion planning problem where the robots are partitioned into groups (colors), such that in each group the robots are interchangeable. Every robot is no longer required to move to a specific target, but rather to some target placement that is assigned to its group. We call this problem k-color multi-robot motion planning and provide a sampling-based algorithm specifically designed for solving it.
At the heart of the algorithm is a novel technique where the \(k\)-color problem is reduced to several discrete multi-robot motion planning problems. These reductions amplify basic samples into massive collections of free placements and paths for the robots.
We demonstrate the performance of the algorithm by an implementation for the case of disc robots and polygonal robots translating in the plane. We show that the algorithm successfully and efficiently copes with a variety of challenging scenarios, involving many robots, while a simplified version of this algorithm, that can be viewed as an extension of a prevalent sampling-based algorithm for the k-color case, fails even on simple scenarios. Interestingly, our algorithm outperforms a well established implementation of PRM for the standard multi-robot problem, in which each robot has a distinct color.
From a theoretic point of view, we show that the algorithm is probabilistically complete when a few simple assumptions are made.
Scenarios
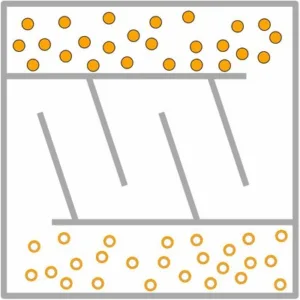
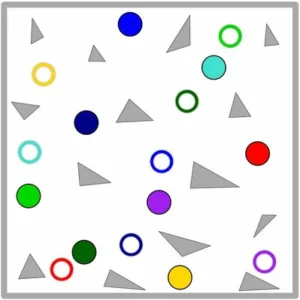
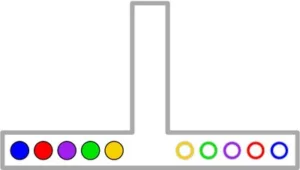
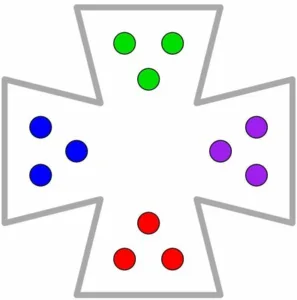
Listed below are challenging scenarios on which we tested the algorithm. Start positions of the robots are indicated by discs while target positions are illustrated as circles in respective colors (unless otherwise indicated) (a) Unlabeled (1-Color) scene with twenty five robots. (b) 2-Color scene; the two groups are required to switch positions. (c) Fully-colored scene with eight robots. (d) Fully-colored scene with five robots. (e) 4-Color scene; every group has to move in a clockwise manner to the next room, e.g., blue group should move to the bottom room.
|
|
|
|
|
|
|