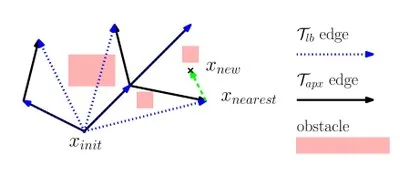
We present Lower Bound Tree-RRT (LBT-RRT), a novel, single-query sampling-based algorithm that is asymptotically near-optimal. Namely, the solution extracted from LBT-RRT converges to a solution that is within an approximation factor of \(1+\epsilon\) of the optimal solution. Our algorithm allows for a continuous interpolation between the fast RRT algorithm and the asymptotically optimal RRT* and RRG algorithms. When the approximation factor is 1 (i.e., no approximation is allowed), LBT-RRT behaves like the RRT* algorithm. When the approximation factor is unbounded, LBT-RRT behaves like the RRT algorithm. In between, LBT-RRT is shown to produce paths that have higher quality than RRT would produce and run faster than RRT* would run. This is done by maintaining a tree which is a sub-graph of the RRG roadmap and a second, auxiliary tree, which we call the lower-bound tree. The combination of the two trees, which is faster to maintain than the tree maintained by RRT*, efficiently guarantee asymptotic near-optimality.
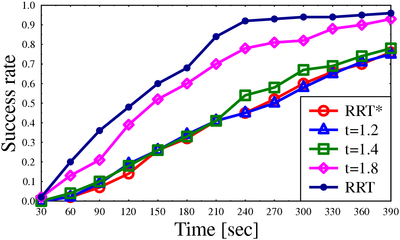
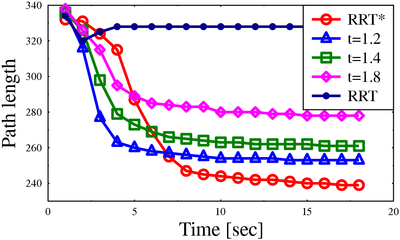
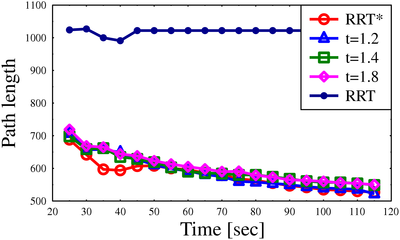
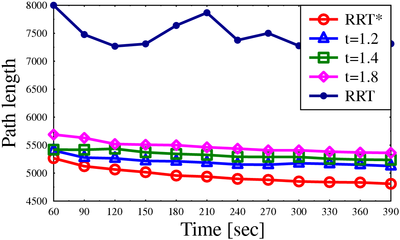
We demonstrate the performance of the algorithm for scenarios ranging from 3 to 12 degrees of freedom and show that even for small approximation factors, the algorithm produces high-quality solutions (comparable to RRT*) with little runtime overhead when compared to RRT.
Experimental results*
Benchmark scenarios. The start and goal configuration are depicted in green and red, respectively
|
|
|
|
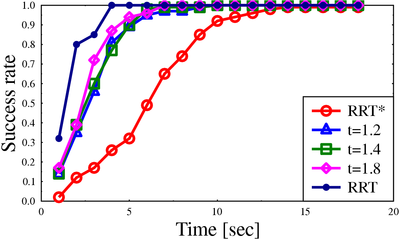
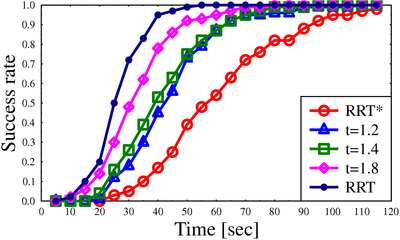
Success rate for algorithms on different scenarios
|
|
|
|
Path lengths for algorithms on different scenarios
|
|
|
|
* Implemented using OMPL, the cubicles and the maze scenarios are provided with the OMPLdistribution.