Sampling-based motion-planning algorithms typically rely on nearest-neighbor (NN) queries when constructing a roadmap. Recent results suggest that in various settings NN queries may be the computational bottleneck of such algorithms. Moreover, in several asymptotically-optimal algorithms these NN queries are of a specific form: Given a set of points and a radius r report all pairs of points whose distance is at most r. This calls for an application-specific NN data structure tailored to efficiently answering this type of queries.
Randomly transformed grids (RTG) were recently proposed by Aiger, Kaplan and Sharir as a tool to answer such queries and have been shown to outperform common implementations of NN data structures in this context.
In this work we employ RTG for sampling-based motion-planning algorithms and describe an efficient implementation of the approach. We show that for motion-planning, RTG allow for faster convergence to high-quality solutions when compared with existing NN data structures. Additionally, RTG enable significantly shorter construction times for batched-PRM variants; specifically, we demonstrate a speedup by a factor of two to three for some scenarios.
Comparison to state-of-the-art nearest-neighbor libraries
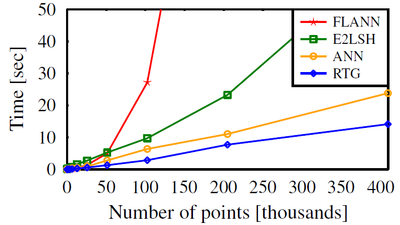
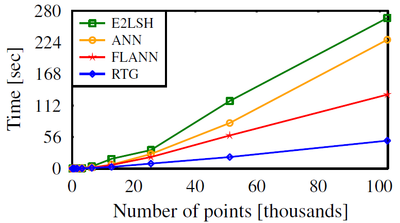
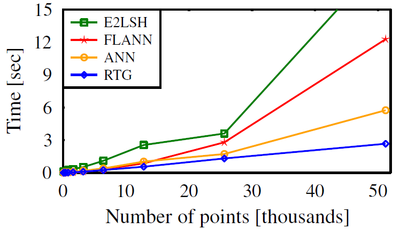
To evaluate our implementation we compared our RTG implementation with the following nearest-neighbor implementations: FLANN kd-tree, ANN kd-tree, and LSH in Euclidean metric spaces (E2LSH).
For each method we measured the time for answering all-pairs r-nearest-neighbors queries for n random uniform samples from the unit \(d\)-dimensional hypercube.
The radius \(r = r(n)\) was defined as follows:
$$r_{\text{FMT}} = 2 (1 + \eta)\left[\left(\frac{1}{d}\right)\cdot \left( \frac{\mu (\chi_{\text{free}})}{\zeta_d} \right) \cdot \left(\frac{\log n}{n} \right)\right]^{1/d}$$
We used point sets, of increasing sizes, of dimensions \(d = 3,6,9, \text{and } 12\).
We performed the same experiment in environment cluttered with obstacles.
The following plots present our results (averaged over ten runs) for different dimensions
|
|
|
|
Motion-planning experiments
For the following experiments we used OMPL, and compared several sampling-based motion-planning algorithms with two possible structures for nearest-neighbors queries: (i) RTG and (ii) GNAT (OMPL’s default).
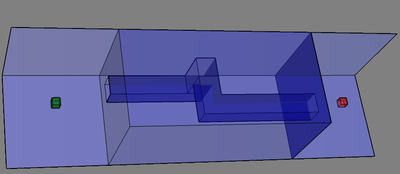
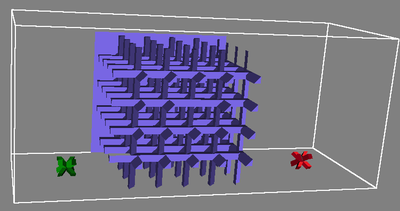
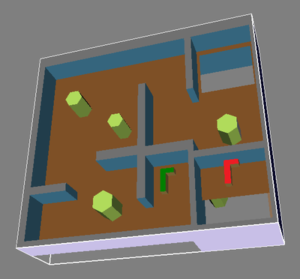
The tested scenarios:
|
|
|
|
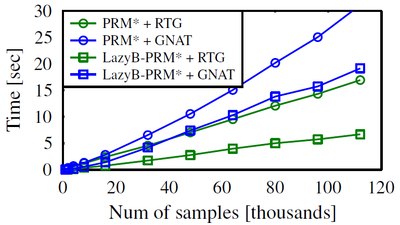
The roadmap construction time as a function of the number of samples for the PRM* algorithm (circle marks) on the Z-tunnel scenario in a 3D C-space (one translating robot in space) using both RTG and GNAT.
A similar experiment was performed for Lazy Batch-PRM* (marked in squares).
For these two experiments we used the Euclidean metric for distance computations.
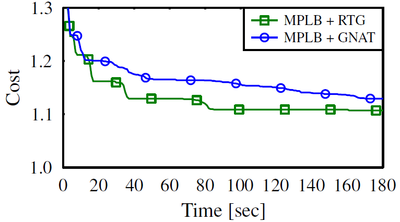
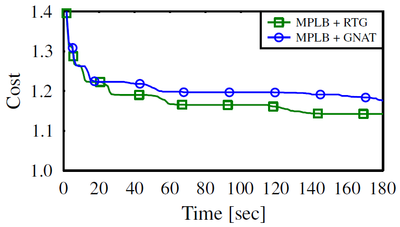
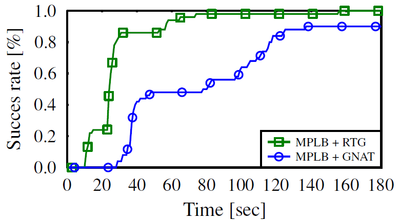
The cost as a function of time for the MPLB algorithm on the 3D Grid scenario in a 6D C-space (two translating robots in space).
The distance metric computes the sum of the distances that each robot travels (Non-Euclidean metric).
The same experiment was performed while using the Euclidean metric instead.
|
|
|
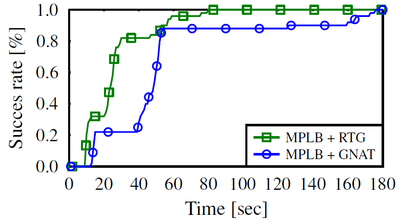
The success rate of finding a solution as a function of time for the MPLB algorithm on the Cubicles scenario in a 6D C-space (using both the Euclidean and the non-Euclidean metrics).
|
|
|
Implementation
Our C++ implementation is available here.
The reference manual can be found here.