We show the exact, efficient, and complete computation of planar arrangements induced by algebraic curves of arbitrary degree. The implementation poses no restrictions on the input, that is, curves may have covertical critical points, several may pass through a common point, or they can overlap. The implementation is based on CGAL’s 2D Arrangement package which provides a generic and complete version of Bentley and Ottmann’s sweep-line algorithm. Its expected geometric constructions and predicates for algebraic curves can be reduced cylindrical algebraic decompositions of the plane for one or two curves. This reduction is implemented in CGAL’s new experimental Curved_kernel_via_analysis_2 package, while the actual analyses are provided by CGAL’s new experimental Algebraic_curve_kernel_2 package. The latter is actually based on a univariate algebraic kernel which basically provides the method for univariate real root isolation. Several models for this task exist. The analyses of curves are computed with the help of a new and efficient method that combines adaptive-precision root finding (the Bitstream Descartes method of Eigenwillig et~al., 2005) with a small number of symbolic computations, and that delivers the exact result in all cases. Thus, we eventually obtain an algorithm which produces the mathematically true arrangement, undistorted by rounding error, for any set of input segments.
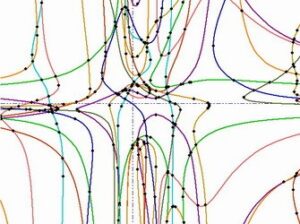
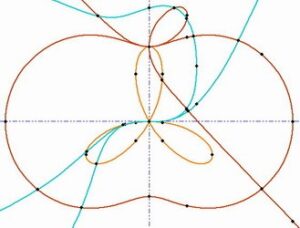
The implementation is also enhanced with a robust visualization for arcs of algebraic curves. Each curve arc is traced separetely in both directions starting from a seed point. In order to distinguish closely located features of the curves we employ a local space subdivision. Robustness of our algorithm is guaranteed by three levels of increasing arithemtic precision (floating-point filtering).
The arrangement computation can be experienced online. We provide a web-based application with Macromedia Flash client interface which allows to compute and visualize exact 2D arrangements of implicit real algebraic curves. We also provide various arrangement data, such as: number of arcs, vertices, isolated vertices and facets. Feature selection mode allows to emphasize on certain arrangement items, i.e., arcs, vertices or facets. It can be used for demonstrative and educational purposes.
