We study a fundamental NP-hard motion coordination problem for multi-robot/multi-agent systems: We are given a graph \(G\) and set of agents, where each agent has a given directed path in \(G\). Each agent is initially located on the first vertex of its path. At each time step an agent can move to the next vertex on its path, provided that the vertex is not occupied by another agent. The goal is to find a sequence of such moves along the given paths so that each agent reaches its target, or to report that no such sequence exists. The problem models guidepath-based transport systems, which is a pertinent abstraction for traffic in a variety of contemporary applications, ranging from train networks or Automated Guided Vehicles (AGVs) in factories, through computer game animations, to qubit transport in quantum computing. It also arises as a sub-problem in the more general multi-robot motion-planning problem. We provide an in-depth tractability analysis of the problem by considering new assumptions and identifying minimal values of key parameters for which the problem remains NP-hard. Our analysis identifies a critical parameter called vertex multiplicity (VM), defined as the maximum number of paths passing through the same vertex. We show that a prevalent variant of the problem, which is equivalent to Sequential Resource Allocation (concerning deadlock prevention for concurrent processes), is NP-hard even when VM is \(3\). On the positive side, for VM \(\leq 2\) we give an efficient algorithm that iteratively resolves cycles of blocking relations among agents. We also present a variant that is NP-hard when the VM is \(2\) even when \(G\) is a 2D grid and each path lies in a single grid row or column. By studying highly distilled yet NP-hard variants, we deepen the understanding of what makes the problem intractable and thereby guide the search for efficient solutions under practical assumptions.
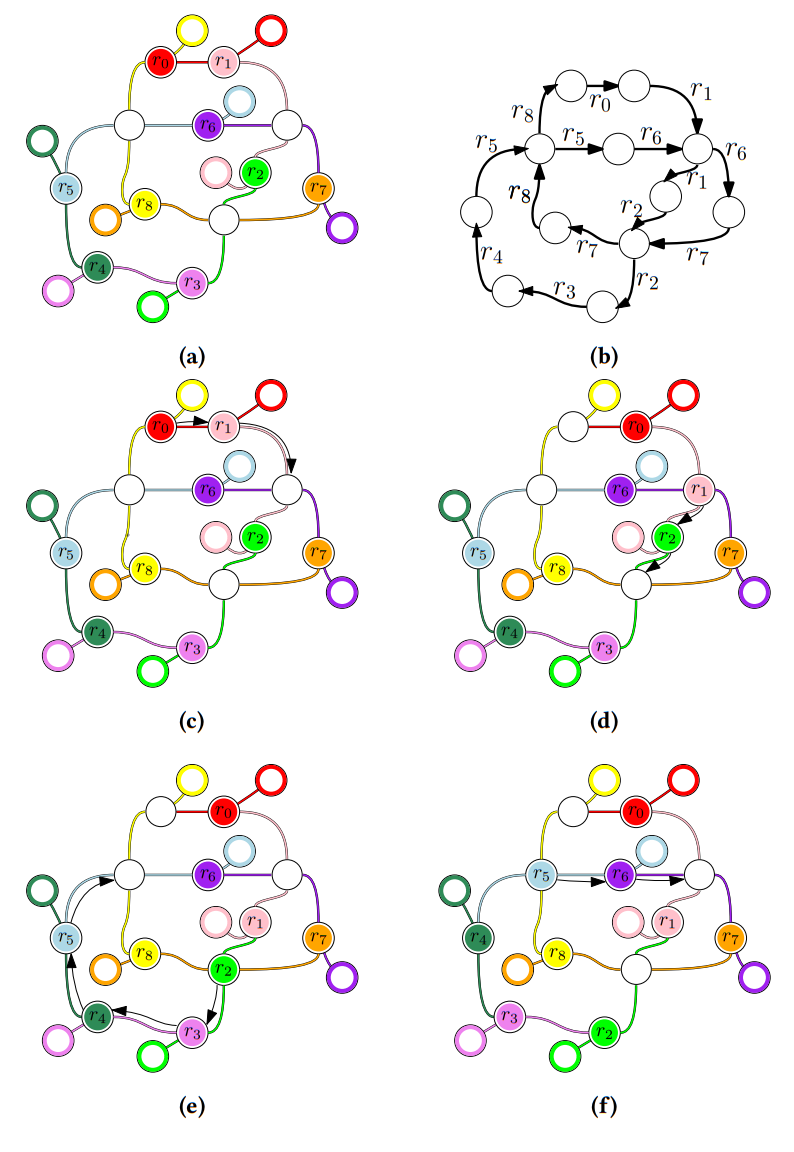
Figure description: (a) An instance with \(9\) robots, each shown as colored filled disk, along with its path in the same color that leads its target. The instance contains a cycle in which each robot is being obstructed by the next one. (b) We convert the instance to an equivalent “graph composed of paths”. We show that if in this graph every simple cycle contains two vertices not occupied by a robot, then the cycle can be solved, as is the case here. (c)-(f) The first \(4\) solution steps as part of solving the instance.
