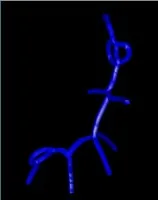
3D printing as a manufacturing system offers new possibilities for designers. The ability to print fully assembled mechanisms, while maintaining the assembly functionalities is desired. Due to the nature of the 3D printing process, in order to 3D-print a mechanism as a whole, some tolerance between the parts must exists, so that the parts do not stick together. This tolerance changes from printer to printer. Eroding (insetting) general 3D parts introduces such a tolerance, and thus presents a solution for this problem. We present an implementation of a method that erodes 3D parts. The implementation consists of two variants based on Nef polyhedra and on Gaussian Maps, respectively. These variants are also compared as part of this project. Eroding of a 3D part can result with a model that cannot be printed (because it is too thin, for example). To this end and to enable automation, validation of the desired offset is discussed and implemented. Finally, a proof of concept for using this solution to print a 3D puzzle, namely the Gordian Knot, is presented; see the figure to the right.
|
|
|
| An example of eroding a 3d model | |
| a. A model of the digit ‘1’. b. A model of the eroded digit ‘1’. |
|
|
|
|
| An example of the skeleton computation exploited by the validation process | |
| a. A model of an elephant. b. A model of the skeleton of the elephant. |
|