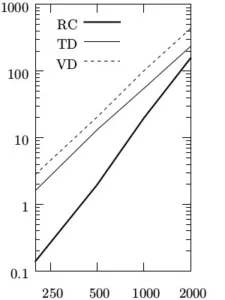
We present an efficient algorithm that computes the Minkowski sum of two polygons, which may have holes. The new algorithm is based on the convolution approach. We also present a simple theorem, related to the Minkowski sum of polygons with holes, exploited by the new algorithm. We introduce a robust implementation of the new algorithm, which follow the Exact Geometric Computation paradigm and thus guarantees exact results. We also present an empirical comparison of the performance of Minkowski sum constructions, where we show that the implementation of the new algorithm exhibits better performance then all other implementations in many cases. In particular, we compared the implementation of the new algorithm, an implementation of the standard convolution algorithm, and an implementation of the decomposition approach using various convex decomposition methods, including two new methods that handle polygons with holes—one is based on vertical decomposition and the other is based on triangulation.
