We study the problem of path planning for unlabeled (indistinguishable) unit-disc robots in a planar environment cluttered with polygonal obstacles. We introduce an algorithm which minimizes the total path length, i.e., the sum of lengths of the individual paths. Our algorithm is guaranteed to find a solution if one exists, or report that none exists otherwise. It runs in time \(O(m^4 + m^2 n^2)\), where \(m\) is the number of robots and \(n\) is the total complexity of the workspace. Moreover, the total length of the returned solution is at most OPT\(+4m\), where OPT is the optimal solution cost. To the best of our knowledge this is the first algorithm for the problem that has such guarantees. The algorithm has been implemented in an exact manner and we present experimental results that attest to its efficiency.
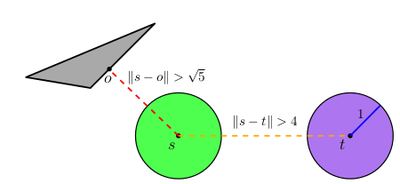
Illustration of the separation conditions assumed in this work. The green and purple discs represent two unit-disc robots placed in a start position \(s\) and goal positions \(t\), respectively. The blue line represents the unit radius of the robot (for scale). The distance between the two positions is at least 4 units (see dashed orange line). The grey triangle represents an obstacle and the point \(o\) represents the closest obstacle point to \(s\). The distance between \(o\) and \(s\) is at least \(\sqrt{5}\) units (see dashed red line).
