|
|
|
|
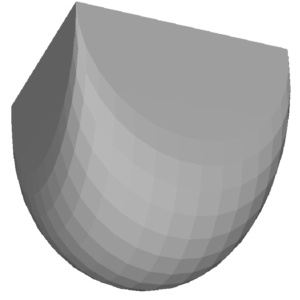
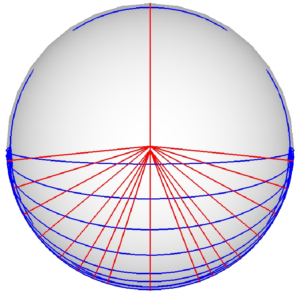
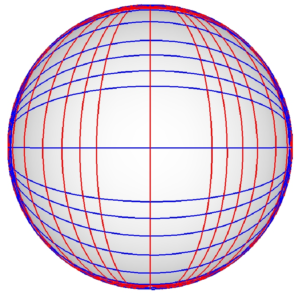
| The Minkowski sum \(M_{11,11} = P_{11} \oplus P’_{11}\), where \(P’_{11}\) is \(P_{11}\) rotated \(90^\circ\) about the vertical axis | ||
We present a tight bound on the exact maximum complexity of Minkowski sums of convex polyhedra in \(\mathbb{R}^3\). In particular, we prove that the maximum number of facets of the Minkowski sum of two convex polyhedra with \(m_1,m_2,\ldots,m_k\) facets respectively is bounded from above by \(\sum_{1 \leq i < j \leq k} (2m_i – 5)(2m_j – 5) + \sum_{1 \leq i \leq k} m_i + \binom{k}{2}\). Given \(k\) positive integers \(m_1,m_2,\ldots,m_k\), we describe how to construct \(k\) polytopes with corresponding number of facets respectively, such that the number of facets of their Minkowski sum is exactly \(\sum_{1 \leq i < j \leq k} (2m_i – 5)(2m_j – 5) + \sum_{1 \leq i \leq k} m_i + \binom{k}{2}\). When \(k = 2\), for example, the expression above reduces to \(4m_1 m_2 −9m_1 −9m_2 +26\). A few pre-constructed polytopes and an interactive program that visualizes them are available at Mink.