We investigate the complexity of the outer face in arrangements of line segments of a fixed length l in the plane, drawn uniformly at random within a square. We derive upper bounds on the expected complexity of the outer face, and establish a certain phase transition phenomenon during which the expected complexity of the outer face drops sharply as a function of the total number of segments. In particular we show that up till the phase transition the complexity of the outer face is almost linear in n, and that after the phase transition, the complexity of the outer face is roughly proportional to \(\sqrt{n}\). Our study is motivated by the analysis of a practical point-location algorithm (so-called walk-along- a-line point-location algorithm) and indeed, it explains experimental observations of the behavior of the algorithm on arrangements of random segments.
Illustrations
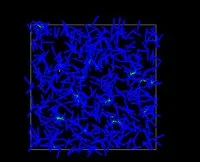
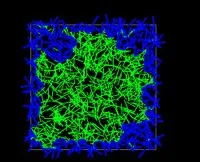
The following illustrations demonstrate phase transition in the number of outer face segments randomly generated in a disc/square.
- Almost all of the outer face segments are near the boundary.
- The outer face segments appear both inside and on the boundary.
- Almost all the segments are on the outer face.
Movies showing the full transition can be downloaded below.
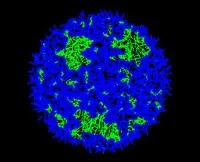
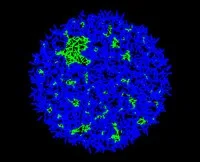
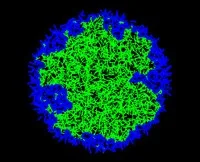
Phase transition in the number of outer face segments randomly generated in a disc