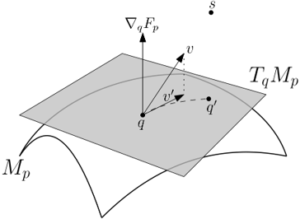
Tight Motion Planning by Riemannian Optimization for Sliding and Rolling with Finite Number of Contact PointsWe address a challenging problem in motion planning where robots must navigate through narrow passages in their configuration space. Our novel approach leverages optimization techniques to facilitate sliding and rolling movements across critical regions, which represent semi-free configurations, where the robot and the obstacles are in contact. Inspired by the human hand, our algorithm seamlessly traverses widely free regions, follows semi-free paths in narrow passages, and smoothly transitions between the two types. We specifically focus on complex scenarios such as tight assemblies, screw-like assemblies, and 3D wire puzzles, all requiring intricate simultaneous translations and rotations. |
 |
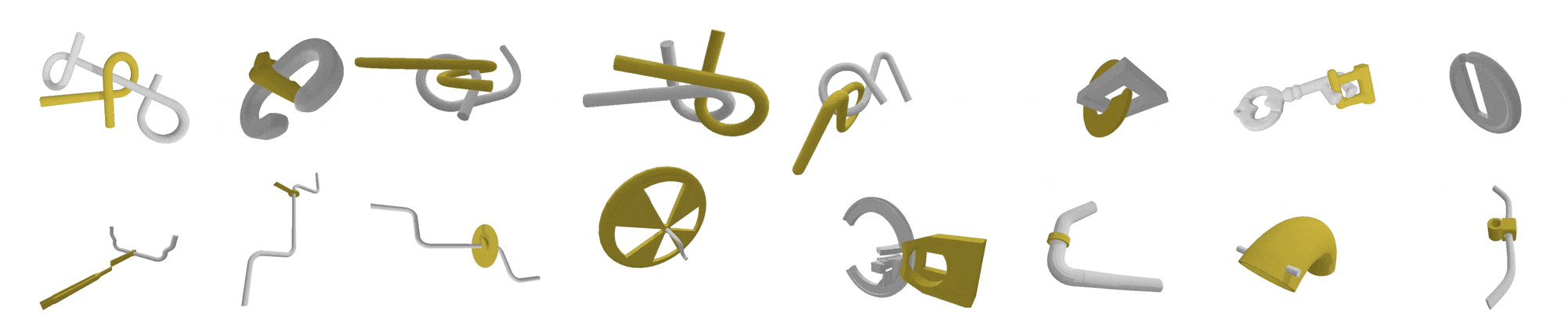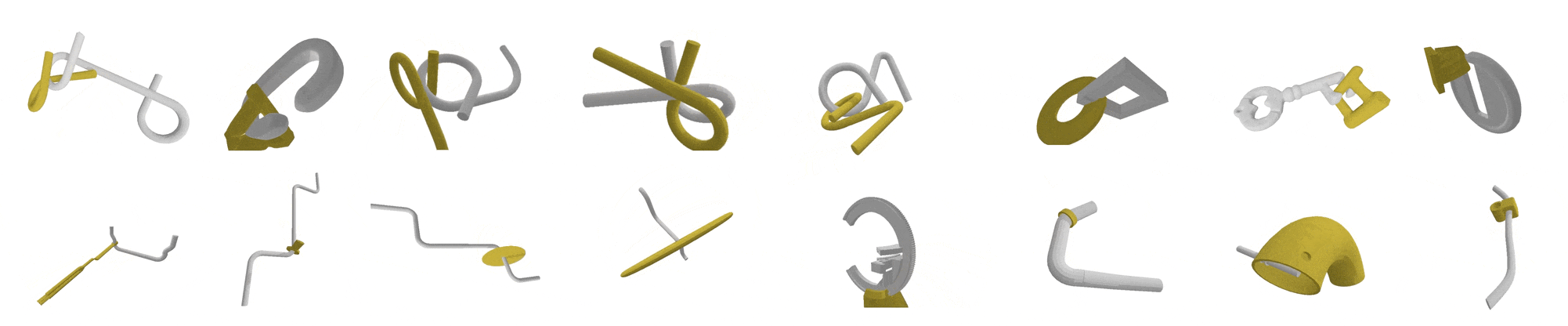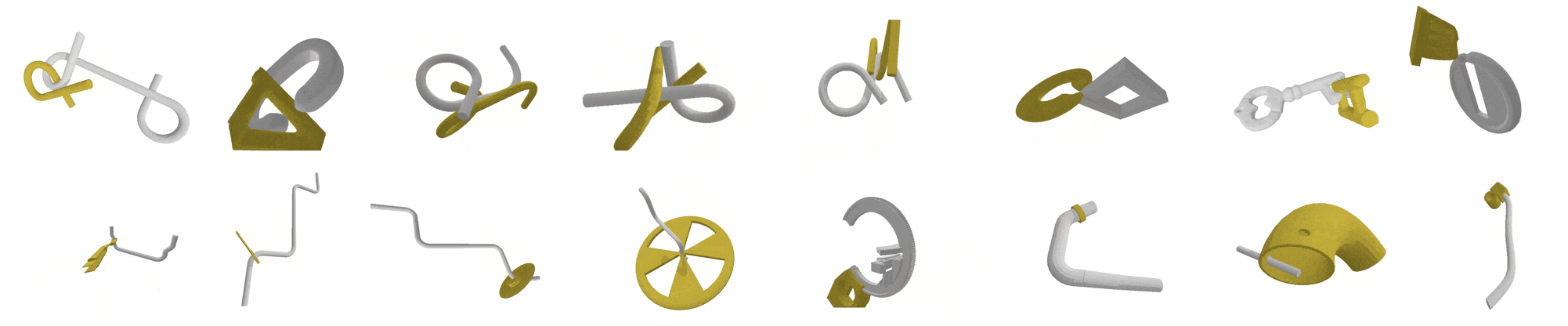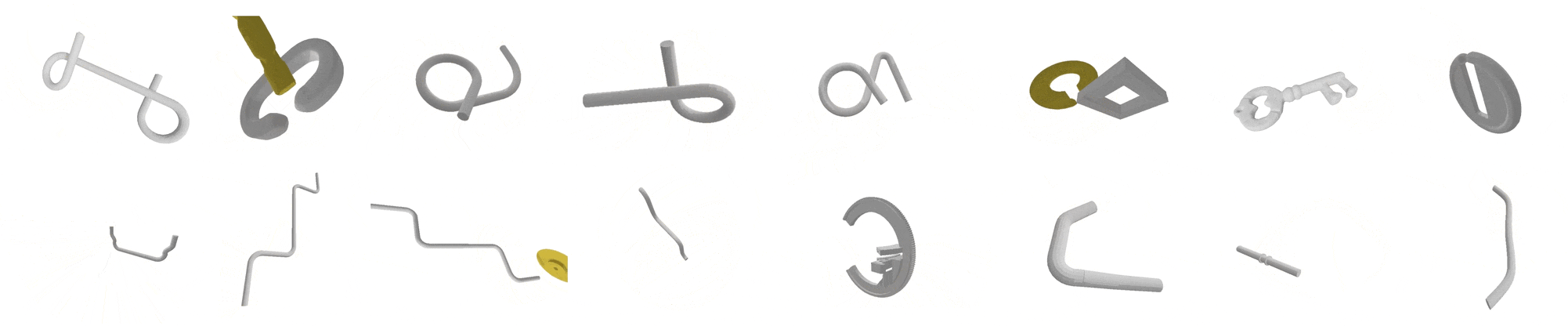 |
 |
 |
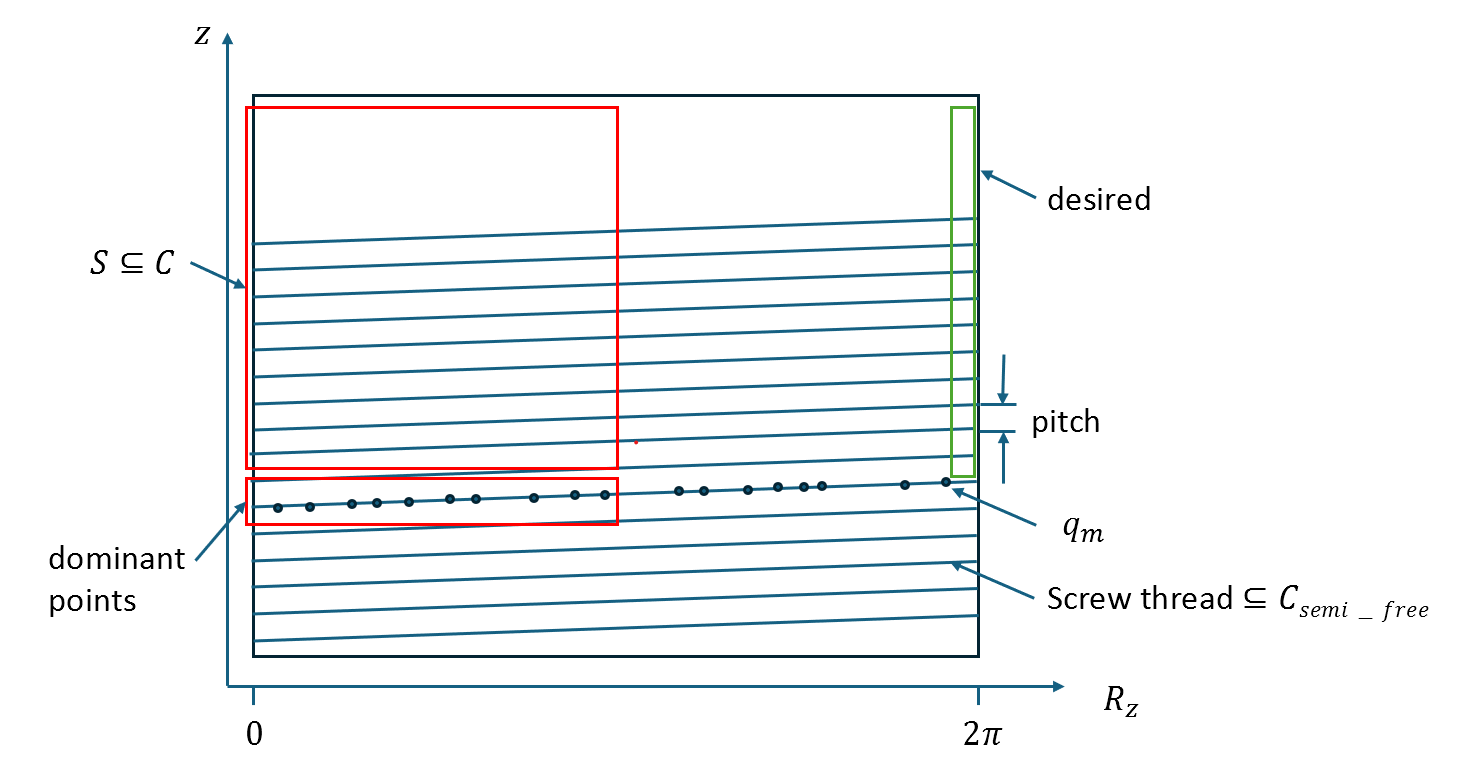 |
Manifold-Guided Motion Planning for Tight AssembliesAbstract. Motion planning for rigid-body assembly poses a fundamental challenge in robotics due to tight geometric constraints. In such scenarios, feasible motions often require passing through (near-)zero clearance configurations in which the parts are tightly constrained by contact. In this work, we introduce Critical-Manifold Guided RRT (CMG-RRT), a sampling-based planner designed specifically for tight assembly problems. Our key observation is that in tight assemblies, valid solution paths lie on or near a critical manifold: the subset of configuration space consisting of poses with at least one contact point between parts. CMG-RRT guides exploration by adaptively biasing sampling toward neighborhoods of the critical manifold using a hierarchical subdivision of the configuration space. We prove that CMG-RRT is probabilistically complete under standard clearance assumptions. Empirical evaluation on challenging rotational assembly benchmarks demonstrates a 100% success rate across all tested instances, including, to the best of our knowledge, the first fully automatic solution of the Elk disentanglement puzzle. The open source for this project is available here. |
 |
